With the completion of the Geological Map of the World it is now a relatively easy process to determine ancient Earth radii using measured surface areas of seafloor crusts. The added advantage of this map is that the seafloor crusts have known ages, which are in turn used to accurately constrain the moment in time when these rocks were first formed.    

The surface area of seafloor crustal stripes is established by digitising directly from the 24-segment sinusoidal map shown below. This sinusoidal map is true-to-scale which means it can be both measured and cut and pasted directly onto a spherical model of the Earth. Once the area of each coloured seafloor crustal stripe is known, the cumulative areas of the seafloor crust—that is, the total area of crusts younger than the time we want to calculate a radius for—is then simply taken away from the present-day Earth surface area to mathematically derive an ancient Earth radius.

24-segment sinusoidal map projection of the Geological Map of the World. This projection enables the geological map to be displayed in distortion-free spherical format and forms the primary base-map for both surface area measurement and small Earth model constructions. This map format can be photocopied and each segment pasted directly onto a spherical globe.

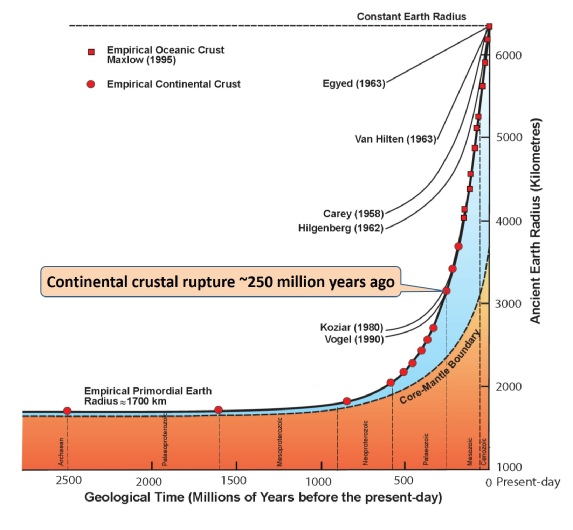
This surface area data is then used to construct small Earth models at ancient radii coincident with the boundaries of each coloured stripe shown. These boundaries, in turn, represent the age distributions of each of the established geological epochs and periods. Models constructed for both seafloor and continental crusts are shown as red dots and squares in the ancient Earth radius graph below.

Exponential increases in Earth radius extending from the Archaean to present-day. Graph shows post-Triassic increase in radius derived from seafloor mapping and pre-Triassic change in radius derived from an Archaean primordial Earth radius of 1700 km. Small Earth models constructed are shown as red coloured circles and squares. A suggested core-mantle boundary remains speculative.

The presence of ancient Precambrian pink and red continental rocks shown in theGeological Map of the World suggests that a primordial small Earth may have existed at the beginning of geological time—around 4,000 million years ago. Since, on an Expansion Tectonic Earth, there were no, or very limited, volcanic seafloor crusts in existence during pre-Triassic times evidence for this primordial Earth radius must then be determined from the distribution of ancient sedimentary basins found on each of the present-day continents.

The method adopted here to determine a potential primordial Earth radius using continental sedimentary basins is basically very simple. During model construction, by moving back in time the radius of each succeeding model is progressively reduced in small, incremental stages. An equivalent area of the youngest sedimentary and magmatic rocks remaining is then removed from the model under construction. The established global network of sedimentary basins is then progressively reduced in surface area until only the most ancientPrecambrian continental crustal rocks remain.

This method is justifiable because the younger crustal rocks represent sedimentary and magmatic rocks that were deposited, intruded, or extruded after the older crustal rocks were first formed. During progressive removal of the younger rocks, each of the sedimentary basins are then restored to a pre-stretching or pre-rift configuration and all sediments and magmatic rocks are simply returned to the exposed land surfaces or mantle where they originated from.

By using this construction method an Archaean small Earth with a primordial Earth radius of about 1,700 kilometres can be readily constructed. This primordial small Earth is made up of an assemblage of the most ancient pink and red coloured Archaean crustal fragments, plus remnant khaki coloured early-Proterozoic crustal rocks.

This 1,700 kilometre Earth radius, while subjective, represents an approximate limiting radius for the most ancient primordial Earth which can then be used to establish a mathematical formula to calculate Earth radius at any moment back or forward in geological time. From this primordial small Earth radius, mathematical modelling studies of Archaean to present-day Earth radius shows that the change in Earth radius increases in accordance with an exponential rate of increase in Earth surface area, as shown in the graph above.

The ancient Earth radius formula is expressed as:

Ra = (R0-Rp)ekt + Rp

Where: Ra = the ancient Earth radius at time t, R0 = the present-day mean Earth radius, Rp = the primordial Earth radius = 1,700 kilometres, e = base of natural logarithm, k = a constant = 4.5366 x 10–9/year.